Height: Difference between revisions
m →Example program: math formula |
m →Example program: spacing |
||
| Line 73: | Line 73: | ||
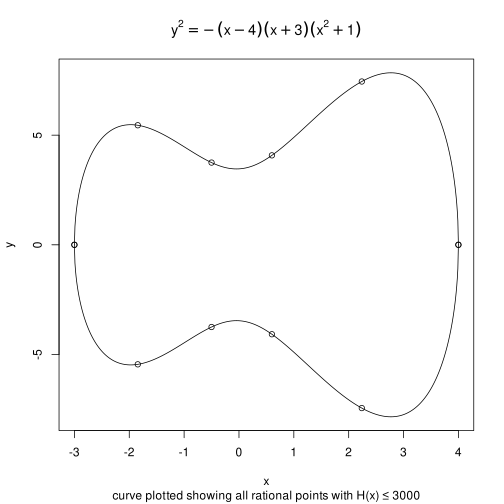
A third curve, <math>y^2=-(x - 4)(x + 3)(x^2 + 1)</math>, does not seem to have any rational points of accessible height at all except for <math>(-3,0)</math>, <math>\left(-\frac{1352}{733}, \pm\frac{2929542}{537289}\right)</math>, <math>\left(-\frac12,\pm\frac{15}{4}\right)</math>, <math>\left(\frac35,\pm\frac{102}{25}\right)</math>, <math>\left(\frac{1077}{481},\pm\frac{1723260}{231361}\right)</math>, and <math>(4,0)</math>. | A third curve, <math>y^2=-(x - 4)(x + 3)(x^2 + 1)</math>, does not seem to have any rational points of accessible height at all except for <math>(-3,0)</math>, <math>\left(-\frac{1352}{733}, \pm\frac{2929542}{537289}\right)</math>, <math>\left(-\frac12,\pm\frac{15}{4}\right)</math>, <math>\left(\frac35,\pm\frac{102}{25}\right)</math>, <math>\left(\frac{1077}{481},\pm\frac{1723260}{231361}\right)</math>, and <math>(4,0)</math>. | ||
[[File:Rational points height 3000.svg]] | [[File:Rational points height 3000.svg]] | ||
Revision as of 06:46, 5 February 2025
The height [1] of a rational number is defined to be the greater of the absolute values of its numerator and denominator in lowest terms.
If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gcd(m,n)=1} , then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle H\left(\frac m n\right) = \max(|m|,|n|)} .
Height is used in the method of infinite descent to prove that some property is true of all rational numbers, when it can be shown that the property is true of any rational number whenever it is true of all rational numbers of lesser height.
Example program
This program will iterate an outer loop over H, the height, and then an inner loop over all rational numbers X = N/D of height H.
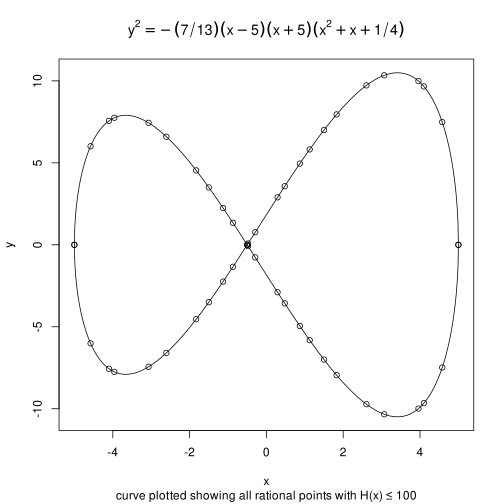
This example outputs all rational points on the curve
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y^2 = -\frac{7}{17}x(x-5)(x+5)(x+1)}
with an x-coördinate whose height does not exceed 1000.
C++. Requires flags “-lgmpxx -lgmp” passed to compiler to link.
#include <iostream>
#include <gmpxx.h> // CMAKE_CXX_FLAGS = -lgmpxx -lgmp
int main(int argc, char **argv) {
mpq_class X, Y, Y2;
mpz_class H, N, D, n, d;
for(H = 1; H <= 1000; ++H) {
for(N = -H, D = 1; D > 0;
N == -H && D < H ? ++D : N < H ? ++N : --D)
{
X.get_num() = N; X.get_den() = D; X.canonicalize();
if (X.get_den() < D) continue; // not in lowest terms
Y2 = mpq_class(-7,17)*X*(X - 5)*(X + 5)*(X + 1);
if (Y2 < 0) continue;
n = sqrt(Y2.get_num()); Y.get_num() = n;
d = sqrt(Y2.get_den()); Y.get_den() = d;
if (Y*Y != Y2) continue;
std::cout << X << ", " << Y << std::endl;
}
}
return 0;
}
-1, 0 0, 0 -5, 0 5, 0 9/5, 168/25 5/16, 525/256 -17/5, 168/25 1/24, 385/576 25/9, 700/81 20/31, 3150/961 -35/27, 1400/729 -85/53, 8400/2809 121/48, 19019/2304 -175/67, 25200/4489 595/131, 115500/17161 -605/129, 77000/16641 -625/601, 231000/361201
Possible conclusions and further questions
- Fairly high rank with many rational points.
- All roots are rational integers.
- Is it too simple?
- What is the algebraic genus of the curve, and how does that affect the cryptographic group operations to be performed on it?
Another curve with a slightly different equation has many, many more rational points.
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y^2 = -\frac7{13}(x-5)(x+5)\left(x^2+x+\frac14\right)}
A third curve, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y^2=-(x - 4)(x + 3)(x^2 + 1)} , does not seem to have any rational points of accessible height at all except for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (-3,0)} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(-\frac{1352}{733}, \pm\frac{2929542}{537289}\right)} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(-\frac12,\pm\frac{15}{4}\right)} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac35,\pm\frac{102}{25}\right)} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\frac{1077}{481},\pm\frac{1723260}{231361}\right)} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (4,0)} .
- ↑ Stephen Hoel Schanuel. “Heights in number fields.” Bulletin de la S. M. F., vol. 107 (1979), p. 433-449. http://www.numdam.org/item/?id=BSMF_1979__107__433_0
